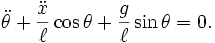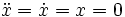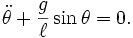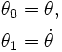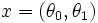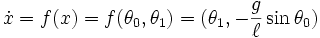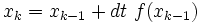Matlab Primer

Today's lecture will be on MATLAB and PENDULA (plural of PENDULUM). Your next lab assignment motivated the topic.

My name is Sean Carver; I am a research scientist in Mechanical Engineering. I have been programming in MATLAB for almost 20 years and programming computers for almost 30 years.

This class is about MATLAB, not about deriving equations. So I am just going to give you the equations for the PENDULUM. There is still a lot to do to get it into MATLAB.

Pendulum on a movable support

This example comes from Wikipedia (copied legally). Consider a pendulum of mass m and length ℓ, which is attached to a support with mass M which can move along a line in the x-direction. Let x be the coordinate along the line of the support, and let us denote the position of the pendulum by the angle θ from the vertical.

Sketch of the situation with definition of the coordinates (click to enlarge)

$\ddot\theta + \frac{\ddot x}{\ell} \cos\theta + \frac{g}{\ell} \sin\theta = 0.\,$

See http://en.wikipedia.org/w/index.php?title=Lagrangian_mechanics&oldid=516894618 for a full derivation.

Your homework and class exercise for today is to implement this model.

Pendulum on a fixed support

Together we are going to implement a simpler model with a fixed and unmovable support. You can easily see how to modify the above equations. Just plug in

$\ddot x = \dot x = x = 0$

The second term drops out:

$\ddot\theta + \frac{g}{\ell} \sin\theta = 0.\,$

Step 1: Make the model first order (first derivatives only)

Define new variables

$\begin{align} \theta_0 & = \theta, \\ \theta_1 & = \dot\theta \end{align}$

Now we have two equations:

$\begin{align} \dot\theta_0 & = \theta_1, \\ \dot\theta_1 & = - \frac{g}{\ell} \sin\theta_0 \end{align}$

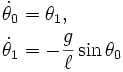
Step 2: Discretize the model

This is a tricky step. Choices must be made. There are many many methods for discretizing a differential equation. There about a dozen MATLAB routines that will do it for you... but then you have to learn how to use them. We will write our own routine implementing the very simplest method...Euler's method.

Euler's Method:

Write the first order variables of the differential equation as a vector:

$x = (\theta_0,\theta_1)$

Write the differential equation as a vector

$\dot x = f(x) = f(\theta_0,\theta_1) = (\theta_1, - \frac{g}{\ell} \sin\theta_0 )$

Now Euler's method is given by the following recursion

$x_k = x_{k-1} + dt \ f(x_{k-1})$

This get translated into the following MATLAB code

theta0(k) = theta0(k-1) + dt * theta1(k-1);
theta1(k) = theta1(k-1) - dt * (g/l)*sin(theta0(k-1));

The whole program

It looks like this

function [theta0,theta1,time] = pend(ang,vel,l,dt,tmax)
% Function to simulate pendulum with length l

g = 9.8;
time = dt:dt:tmax;
kmax = length(time);

% Need to initialize vectors; otherwise runs slowly
theta0 = zeros(1,kmax);
theta1 = zeros(1,kmax);

% Put in initial conditions
theta0(1) = ang;
theta1(1) = vel;

for k=2:kmax
   theta0(k) = theta0(k-1) + dt * theta1(k-1);
   theta1(k) = theta1(k-1) - dt * (g/l)*sin(theta0(k-1));
end
end

Copy and paste the above code into your MATLAB editor, then save as pend.m.

Running the program and plotting results

Run the pendulum code the following pasted into your MATLAB command window:

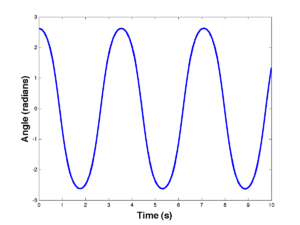
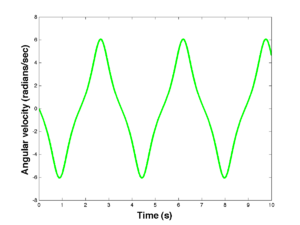
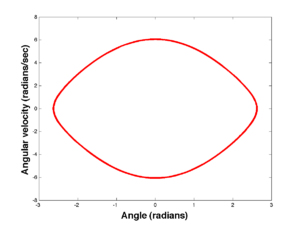
[theta0,theta1,time] = pend(5*pi/6,0,1,.0001,10);
figure(1)
plot(time,theta0,'b');
figure(2)
plot(time,theta1,'g');
figure(3)
plot(theta0,theta1,'r');

You can add axis labels to your plots. First bring the plot to the front then add the labels:

figure(3)
xlabel('Angle (radians)');
ylabel('Angular velocity (radians/sec)');

Now add the axis labels to the others. This is what you should see:

Time versus angle (click to enlarge)

Time versus angular velocity (click to enlarge)

Angle versus angular velocity (click to enlarge)

If you want to put two or more plots on the same figure use:

plot(**First plot**)
hold on
plot(**Remaining Plots**)

Then if you want to erase:

hold off
plot(**New plot**)

Animating the Pendulum

Interpreting the above plots can be hard at first. What we would really like to do is see the pendulum move. I will show you how.

Here is the code that animates the pendulum: (Copy and paste into a new function in the MATLAB editor)

function animate_pend(skip,time,theta0)
% animate_pend -- Function to animate pendulum(assumes length=1)
%    Time may be discretized too finely, so we "skip" frames

figure(1);
kmax = length(time);
for k = 1:skip:kmax
   hold off
   Pshaft = plot([0,sin(theta0(k))],[0,-cos(theta0(k))],'r');
   hold on
   Panchor = plot(0,0,'r*');
   Pmass = plot(sin(theta0(k)),-cos(theta0(k)),'ro');
   set(Panchor,'MarkerSize',20)
   set(Pshaft,'LineWidth',4);
   set(Pmass,'MarkerSize',20);
   axis equal
   axis([-2,2,-2,2])
   set(gca,'XTick',[]);
   set(gca,'YTick',[]);
   getframe(gcf);
end
end

Now generate some data and animate it:

[theta0,theta1,time] = pend(5*pi/6,0,1,.0001,10);
animate_pend(100,time,theta0);

Questions

• We use a very small time step (the variable dt). Smaller means more accurate, but also more expensive to compute. What happens when we increase the time step?

• Return to a small time step and try (initial angle, ang=pi), (initial angular velocity, vel = 1). What is different about this trajectory?