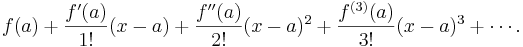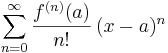Difference between revisions of "Taylor Series"
From Sean_Carver
(→New Concept: Taylor Series) |
(→New Concept: Taylor Series) |
||
| Line 14: | Line 14: | ||
Definition from | Definition from | ||
| − | The Taylor series of a | + | The Taylor series of a function ''ƒ''(''x'') at ''a'' is the power series |
<!-- | <!-- | ||
Revision as of 20:44, 14 March 2011
Review Concepts
- Sequences
- Convergence
- Infinite series
- The sequence of partial sums of an infinite series
- Power series
New Concept: Taylor Series
- Think of Taylor series as a special kind of power series, where the sequence of partial sums are meant as better and better approximations of some other function.
- The Taylor Series is derived from the function.
Definition from
The Taylor series of a function ƒ(x) at a is the power series
which can be written in the more compact sigma notation as
where n! denotes the factorial of n and ƒ (n)(a) denotes the nth derivative of ƒ evaluated at the point a. The zeroth derivative of ƒ is defined to be ƒ itself and Template:Nowrap and 0! are both defined to be 1. In the case that Template:Nowrap, the series is also called a Maclaurin series.