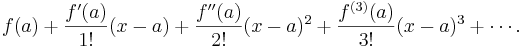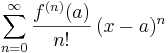Taylor Series

This lecture was delivered in February 2011 to the Department of Mathematics and Statistics search committee at the University of Maryland, Baltimore County. I taught the class to illustrate the teaching methods I developed for the Modeling and Identifying Neurosystems class that I taught at the Johns Hopkins university in Spring of 2009. The topic Taylor Series was assigned to me the night before.

Review Concepts

• Sequences
• Convergence of infinite sequences
• Infinite series
• The sequence of partial sums of an infinite series
• Power series

New Concept: Taylor Series

• Think of Taylor series as a special kind of power series, where the sequence of partial sums are meant as better and better approximations of some function.
• The Taylor Series is derived from the function.

Definition copied, verified, and adapted from Wikipedia, this page (permanent link). See license to copy, modify, distribute. Also adapted somewhat based on textbook Finney & Thomas, Calculus, 2nd edition.

Let f be a function with derivatives of all orders throughout some interval containing a as an interior point. The Taylor series of the function ƒ(x) at a is the power series

$f(a)+\frac {f'(a)}{1!} (x-a)+ \frac{f''(a)}{2!} (x-a)^2+\frac{f^{(3)}(a)}{3!}(x-a)^3+ \cdots.$

which can be written in the more compact sigma notation as

$\sum_{n=0} ^ {\infin } \frac {f^{(n)}(a)}{n!} \, (x-a)^{n}$

• Note that for nth approximate partial sum, the only information used about the function 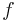$f$, is its derivatives at 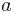$a$ up to order $n$.
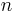• Convergence: A function whose Taylor series converges to the function is called analytic. But sometimes, as we have seen with power series generally, convergence can occur only within a radius of convergence.
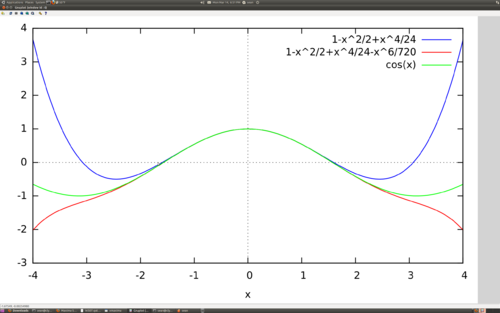
• Example: The Taylor series for cos(x), at a = 0. Partial sums for 4 and 6 terms.

cos(x) and Taylor series partial sums for cos(x), 4 and 6 terms

Try it yourself

Open Maxima and type (or copy and paste):

a:0;
n1:4;
n2:6;
M:4;
plot2d([taylor(cos(x),x,a,n1), taylor(cos(x),x,a,n2), cos(x)],[x,-M,M]);

After you have typed in the above you can change the parameters a, n1, n2, M by scrolling up and changing them, then pressing return.

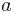• $a$ is where the derivatives are taken (center)
• n1 and n2 are the orders for the two taylor series plots
• [-M, M] is the range of the plot

Questions for Exploration and Discussion in Groups of Three (With Computer)

• Does the series seem to converge in the range [-M,M] =[-8,8]? If so, how large should n1 or n2 be so that this convergence is apparent?

• What is imprecise about the previous question? Why should it make a mathematician cringe? Can you fix the problem?

Instead of cos(x) try the function

$f(x) = \frac{1}{x^2+1}$

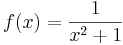
plot2d([taylor(1/(x^2+1),x,a,n1), taylor(1/(x^2+1),x,a,n2), 1/(x^2+1)],[x,-M,M]);

• Is there an interval where the Taylor series seems to converge? What is it?

• Use the formula above to compute (by hand) the Taylor series to order 4 (i.e. n=4) of 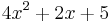$4 x^2 + 2 x + 5$ at the point a=1.

Looking Ahead

• Taylor's theorem -- a precise statement about the error in a Taylor approximation of f(x) (ie. a partial sum of the Taylor series of f(x)).