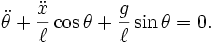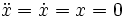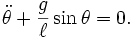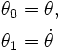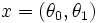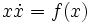Difference between revisions of "Matlab Primer"
(→Step 2: Discretize the model) |
(→Step 2: Discretize the model) |
||
| Line 45: | Line 45: | ||
:<math> x = (\theta_0,\theta_1) </math> | :<math> x = (\theta_0,\theta_1) </math> | ||
| + | |||
| + | Write the differential equation as a vector | ||
| + | |||
| + | :<math> x \dot x = f(x) </math> | ||
Revision as of 19:08, 3 November 2012
Today's lecture will be on MATLAB and PENDULA (plural of PENDULUM). Your next lab assignment motivated the topic.
My name is Sean Carver; I am a research scientist in Mechanical Engineering. I have been programming in MATLAB for almost 20 years and programming computers for almost 30 years.
This class is about MATLAB, not about deriving equations. So I am just going to give you the equations for the PENDULUM. There is still a lot to do to get it into MATLAB.
Contents
Pendulum on a movable support
This example comes from Wikipedia (copied legally). Consider a pendulum of mass m and length ℓ, which is attached to a support with mass M which can move along a line in the x-direction. Let x be the coordinate along the line of the support, and let us denote the position of the pendulum by the angle θ from the vertical.
See http://en.wikipedia.org/w/index.php?title=Lagrangian_mechanics&oldid=516894618 for a full derivation.
Your homework and class exercise for today is to implement this model.
Pendulum on a fixed support
Together we are going to implement a simpler model with support fixed and unmovable. You can see what the equations for this are easily. Just plug in
The second term drops out:
Step 1: Make the model first order (first derivatives only)
Define new variables
Now we have two equations:
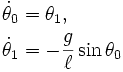
Step 2: Discretize the model
This is a tricky step. Choices must be made. There are many many methods for discretizing a differential equation. There about a dozen MATLAB routines that will do it for you... but then you have to learn how to use them. We will write our own routine implementing the very simplest method...Euler's method.
Euler's Method:
Write the first order variables of the differential equation as a vector:
Write the differential equation as a vector