DiffEqs

Plain Bilayer Membrane

Remember the capacitor equation:

$C \frac{dV(t)}{dt} = I(t)$

$V(0) = 0$

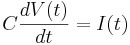
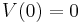
Here C is a constant (a parameter): the capacitance of the membrane.

Next V(t) is the membrane potential. Typically V(t) is the quantity of interest -- and it is the quantity that is usually measure.

Next I(t) is the capacitive current into the cell. In general the capacitive current involves the ionic currents into the cell as well as the injected current, but for a plain lipid bilayer, it is just the injected current.

Finally V(0) is the initial membrane potential of the cell, the constant of integration required for a definite solution to the equation.

We can solve this equation

$V(t) = V(0) + \frac{1}{C} \int_0^t I(s) ds$

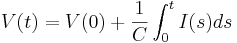
Add Na+/K+ Pump

It seems clear from the Neurons in Action Tutorial that they modeled the addition of the pump as a change in the initial condition of the cell.

$C \frac{dV(t)}{dt} = I(t)$

$V(0) = -75$

$V(t) = V(0) + \frac{1}{C} \int_0^t I(s) ds$

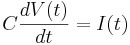
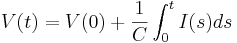
Add Leak Channels

$C \frac{dV}{dt} = I(t) - g_L (V - E_L)$

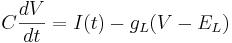
Leak channels add a resistor in parallel to the capacitor.

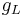$g_L$ is the conductance of the channels (which is the reciprocal of the resistance of the channels).

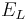$E_L$ is the reversal potential of the leak current.

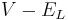$V - E_L$ is the driving potential.

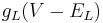$g_L (V - E_L)$ is the current across the resistor (Ohm's Law).

The resistive current is minus its contribution to the capacitive current (Kirchov's Law).

Add HH Channels

$C \frac{dV}{dt} = I(t) - g_L (V(t) - E_L) - g_{Na} m^3(t) h(t) (V(t) - E_{Na}) - g_K n^4(t) (V(t) - E_K)$

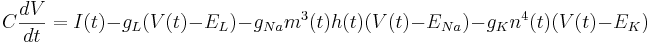
In addition to the leak current there is now a sodium current and a potassium current. These add similar terms to the capacitive current:

Leak: 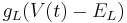$g_L (V(t) - E_L)$

Sodium: 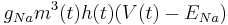$g_{Na} m^3(t) h(t) (V(t) - E_{Na})$

Potassium: 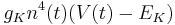$g_K n^4(t) (V(t) - E_K)$

Sodium gating variables: 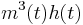$m^3(t) h(t)$

Potassium gating variables: 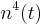$n^4(t)$

Sodium has three activation gates (m's) and one inactivation gate (h).

Potassium has four inactivation gates (n's).

The activation variables m(t), h(t), n(t) are always (for all times t) numbers between 0 and 1. They represent the fraction of gates that are in the open position. All four gates must be open for the channel to conduct. If n = 0.1