Selection

First, the homework from Lab W.

What is Model Selection?

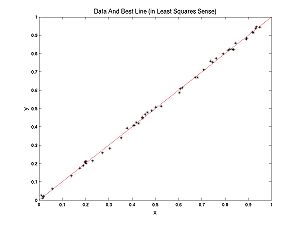
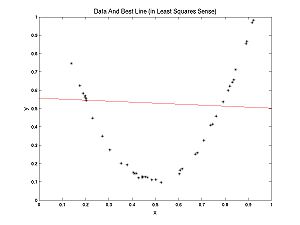
What is model selection? To answer this question let's contrast model selection with parameter estimation. In the Optimization Lab, we fit lines to data. We were doing parameter estimation, trying to estimate the parameters m and b, in the formula for a line y = m*x + b. Recall my examples: we fit a line to nearly linear data and another line to nearly parabolic data.

Fitting a line to nearly linear data. Click for full size image

Fitting a line to nearly parabolic data. Click for full size image

Clearly, in the second case, it would be more appropriate to fit a parabola to the data, rather than a line. How would we do that?

A parabola is described by the formula: 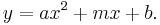$y = a x^2 + m x + b.$ This is a line with a new term, 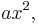$a x^2,$ added. To fit a parabola the procedure is almost the same. First determine the errors in the data:

$Error(x,y,a,m,b) = a x^2 + m x + b - y$

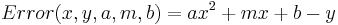
Now define the penalties, (let's be sensible and use LS rather the UG penalties):

$Penalty(x,y,a,m,b) = Error(x,y,a,m,b)^2$

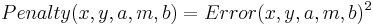
And finally the cost function

$Cost(a,m,b) = \sum_{data} Penalty(x,y,a,m,b)$

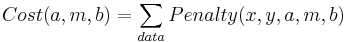
Now we tweak the three parameters (a,m,b) using, for example, the Nelder-Meade method we studied last week. Of course MATLAB has its own routines for solving this problem based on Linear Algebra that are much better than Nelder-Meade.

What if we fit a parabola to the nearly linear data? Note that if we set a = 0, we get y = m*x + b again. Thus a line is a parabola. But there was some noise in the data, so if you are allowed to tweak the parameter a as well as m and b, you can expect a better (lower cost) fit (you are guaranteed that the fit is no worse). So why should we bother fitting lines to data? Why not just always fit parabolas?

But wait, why stop at parabolas? An nth degree polynomial has the form:

$y = a_n x^n + a_{n-1} x^{n-1} + \dots + a_1 x + a_0$

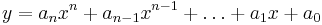
For example, a 0th degree polynomial is a constant function, 1st degree is a line, 2nd degree is parabola, etc. If we have m data points a (usually unique) polynomial of degree m-1 will fit exactly with no error. Some (no longer unique) higher degree polynomials will also fit with no error.

So why don't we fit with a high enough polynomial so that there is no error? If we have 100 data points, use a 99 degree polynomial! No error!