Optimization
First, we discuss homework from Lab V.
Now on to today's topic.
What is Optimization
Given a function that depends upon parameters, find the value of the parameters that optimizes the function (e.g. if the function is likelihood, find the maximum likelihood).
Minimizing functions is trivially the same thing as maximizing functions. Most optimization routines are written to minimize function; if you want to maximize log-likelihood with such a function, you can just minimize minus-log-likelihood. Putting a minus sign in front of the function turns the surface upside down and cost next to nothing computationally.
No Free Lunch!
What is the best optimization routine to use? The "no free lunch" theorem tells you that it doesn't exist; or rather it depends upon your problem. As a result there is a wide diversity of different algorithms that are used in practice. Consider the following rather famous news group post that describes many of the algorithms in a funny way. (OK many of the jokes are inside jokes that only make sense if you already know the algorithms, but the post at least gives you a flavor of the diversity of optimization algorithms.) The post can be found here.
Our Problem
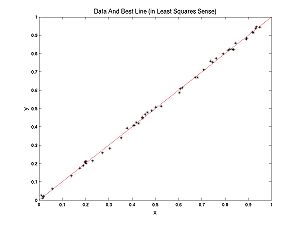
We have some data in the (x,y) plane. Here we consider x to be the independent variable and y to be the dependent variable. Our optimization problem is to find the line y = m*x + b that best fits the data.
Here is some data with the best fitting line.
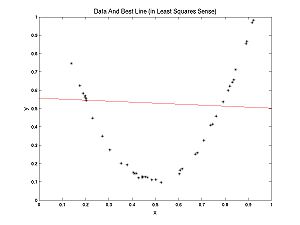
In this case, a line fits well. In the following example a parabola fits better than a line, but we can still ask, what's the best line? The best line is shown:
What determines the best line? Each (x,y) pair from the data has an error associated with it for any given parameter pair (m,b): Error(x,y,m,b) = mx + b - y. Each parameter pair (m, b) has a cost associated with it. Customarily this cost is almost always defined as:
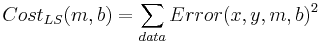
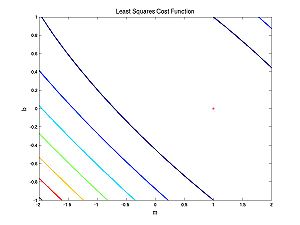
What does this cost function look like as a function of the parameters?
The first case (nearly linear data):
And the second case (nearly parabolic data):
Note that both of these cost functions are very well behaved. Fitting a line to data using a least squares (LS) cost function is a very well behaved problem. To give you an idea of what can happen in more general scenarios (i.e. perhaps with maximum likelihood applied to neural models), I have cooked up a different cost function:
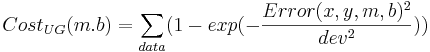
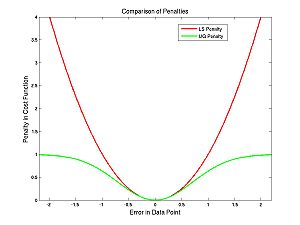
The difference between the cost functions is how they penalize errors. The LS cost function uses squared error whereas the UG one uses an upside-down Gaussian: