Bayesian Filtering

Here is the problem -- there is an open state (O) and closed state (C) and a stuck (inactivated) state (S). Transitions between these states happen like this

$O \rightleftharpoons C \rightleftharpoons S$

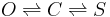
Transitions between O and S never happen (i.e. the probability is negligible) without C being an intermediary state. The observed current is zero in C and S and one in O. And there is noise. Transitions between C and S are invisible because there is no change in current. We want to estimate the transition probabilities. (The probabilities will depend upon the time step, but say the time step is fixed).

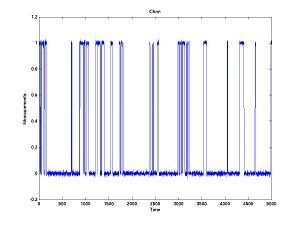
First generate some data which looks like.

Click image for full size

The transition probabilities for this plot are

Probability(Stay in Open) = 0.95
Probability(Open --> Closed) = 0.05
Probability(Open --> Stuck/Inactive) = 0.00

Probability(Closed --> Open) = 0.10
Probability(Stay in Closed) = 0.85
Probability(Closed --> Stuck) = 0.05

Probability(Stuck --> Open) = 0.00
Probability(Stuck -- Closed) = 0.003
Probability(Stay in Stuck) = 0.097

There are nine parameters here, but there is a constraint that each block add to 1, so we only have 6 parameter to estimate. Moreover we might know that transition between open and stuck never happen, so there would only be 4 parameters to estimate.

Thus the likelihood function is a function from four parameters to one value (likelihood). Too many to plot. Let's say we know the probabilities of going back and forth between open and closed. Thus we need only know the probabilities of going back and forth between closed and stuck (the invisible transitions).

We are going to compute the likelihood as we vary

P(Stuck --> Closed) from 0.001 to 0.010
P(Closed --> Stuck) from 0.01 to 0.12

Actually, the way I wrote the program it computes

P(Stuck --> Closed) from 0.001 to 0.010
P(Stay in Closed) from 0.01 to 0.12

The two are equivalent because P(Closed --> Open) is correctly known and the three "from Closed" probabilities add to 1.

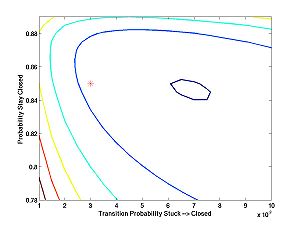
Here are what it looks like:

Click image for full size

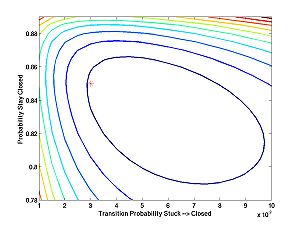
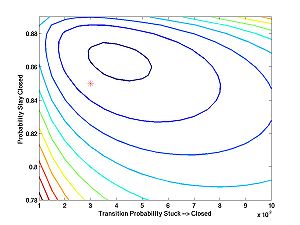
And with two different seeds:

Click image for full size

Click image for full size

I was concerned about the first plot, until I plotted the next two. Then I realized that the algorithm tries to estimate the probabilities of relatively rare events based on a limited amount of data (5000 data points). The performance may not look great at first sight, but consider how subtle are the inferences that it is trying to make. The estimates are reasonably close ... at least within the ballpark. It would look better zoomed out. With a lot more data, one can expect the estimates to be much better.

The purpose of the lecture is to present the Bayesian filtering algorithm.

Prerequisites

• You need to know (or guess) initial probabilities for each state. For example say we assume with certainty that the channel starts open. Then P(X0 is Open) = 1, P(X0 is Closed) = 0, P(X) is Stuck) = 0.

• You need transition probabilities: p_ij is the probability of going to state j, assuming you start in state i.

• You need to know the probability density function for the data given that you are in each state. For example, in the code, densities are Gaussian, the means are (1,0,0) for (open, closed, stuck) and the standard deviation for all is 0.01. In this case the means for open and closed/stuck are separated by 100 standard deviations -- you assume essentially no measurement noise.

• You need the data.

Step One: Start with Initial Probabilities for State And Make a Prediction for Next Time Step

Initial Probabilities

$P(X_0 = i)$

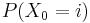
Predicted Probabilities

$P(X_1 = j) = \sum_i P(x_0 = i) p_{ij}$

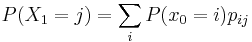
For example, the predicted probability that you are in CLOSED after the first time step (but before more information is gathered) is

• Probability that you start OPEN times probability that you transition from OPEN to CLOSED

• PLUS Probability that you start CLOSED times probability that you stay CLOSED

• PLUS Probability that you start STUCK times probability you transition from STUCK TO CLOSED

Same formula for the other states (OPEN AND STUCK).

Step Two: Collect data, and evaluate probability density of the data

You are computing P(data|state) for each value of state.

Step Three: Weight the densities above by the prior probabilities of being in each state

You are computing P(data|state)*P(state).

Step Four: Sum the weighted densities

This sum is the marginal likelihood. As this step is repeated, the likelihood is the product of all marginal likelihoods. (Actually the log-likelihood is usually computed as the sum of the logs of the marginal likelihoods).

Step Five: Compute the Posterior Probability Mass Function for State Given the Measurement

This is done by normalizing (dividing) the weighted densities by the marginal likelihood.

Repeat Steps One through Five until the data is exhausted

Use the Posterior Mass Function instead of the Initial Probability Mass Function.

Homework

Homework T.1: Repeat data points of zero (expected if Closed or Stuck). What happens to the relative probabilities of closed and stuck in the Posterior PMF as the number of zero data points increases? What happens to the prediction PMF as the number of zero data points increases? What happens if a data point = 1 is thrown in?

Homework T.2: What happens if a data point of 0.5 is thrown in? Recall the standard deviation of the noise (0.01). How many standard deviations away from the mean of 0 or 1 is 0.5. What happens to the marginal likelihood.