Difference between revisions of "Threshold"

From Sean_Carver
Jump to: navigation, search
(→‎Equilibrium Potentials)
Line 24: Line 24:
  
 
Now we can talk about the [[Media:Lab_F.pdf|homework due Monday night]].
 
Now we can talk about the [[Media:Lab_F.pdf|homework due Monday night]].
 +
 +
And the homework due [[Media:Lab G.pdf|Wednesday night]].

Revision as of 18:53, 19 February 2009

Tuesday's lecture has been postponed for today due to a projector malfunction.

Equilibrium Potentials

Recall the equation for the membrane potential in the Hodgkin-Huxley model:

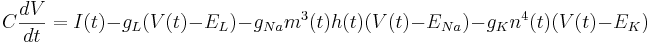
C \frac{dV}{dt} = I(t) - g_L (V(t) - E_L) - g_{Na} m^3(t) h(t) (V(t) - E_{Na}) - g_K n^4(t) (V(t) - E_K)

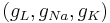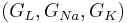You can find the equilibrium potential for given channel conductances. Set the injected current to zero I = 0. Then fix and absorb the gating variables and maximal conductances (g_L, g_{Na}, g_{K}) into single conductance variables (G_L, G_{Na}, G_{K}) .

For example

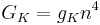
G_{K} = g_K n^4

Then the differential equation for the membrane is

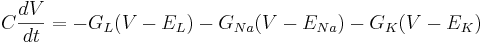
C \frac{dV}{dt} = - G_L (V - E_L) - G_{Na} (V - E_{Na}) - G_K (V - E_K)

The equilibrium potential is the value of V such that 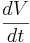\frac{dV}{dt} is zero. You can plug in 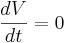\frac{dV}{dt} = 0 and solve for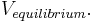 V_{equilibrium}.

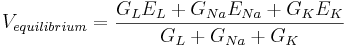
V_{equilibrium} = \frac{G_L E_L + G_{Na} E_{Na} + G_K E_K}{G_L + G_{Na} + G_K}

The equilibrium potential is the weighted average of the reversal potentials -- weighted by the corresponding conductances. Note that the weights add to one.

Now we can talk about the homework due Monday night.

And the homework due Wednesday night.

Retrieved from "https://seancarver.org/index.php?title=Threshold&oldid=442"