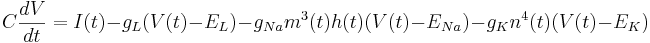Difference between revisions of "DiffEqs"
(→Add HH Channels) |
(→Add Leak Channels) |
||
| Line 32: | Line 32: | ||
<math> C \frac{dV}{dt} = I(t) - g_L (V - E_L) </math> | <math> C \frac{dV}{dt} = I(t) - g_L (V - E_L) </math> | ||
| + | |||
| + | Leak channels add a resistor in parallel to the capacitor. | ||
| + | |||
| + | <math> g_L </math> is the conductance of the channels | ||
== Add HH Channels == | == Add HH Channels == | ||
<math> C \frac{dV}{dt} = I(t) - g_L (V(t) - E_L) - g_{Na} m^3(t) h(t) (V(t) - E_{Na}) - g_K n^4(t) (V(t) - E_K) </math> | <math> C \frac{dV}{dt} = I(t) - g_L (V(t) - E_L) - g_{Na} m^3(t) h(t) (V(t) - E_{Na}) - g_K n^4(t) (V(t) - E_K) </math> | ||
Revision as of 22:42, 10 February 2009
Plain Bilayer Membrane
Remember the capacitor equation:
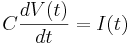
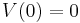
Here C is a constant (a parameter): the capacitance of the membrane.
Next V(t) is the membrane potential. Typically V(t) is the quantity of interest -- and it is the quantity that is usually measure.
Next I(t) is the capacitive current into the cell. In general the capacitive current involves the ionic currents into the cell as well as the injected current, but for a plain lipid bilayer, it is just the injected current.
Finally V(0) is the initial membrane potential of the cell, the constant of integration required for a definite solution to the equation.
We can solve this equation
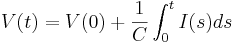
Add Na+/K+ Pump
It seems clear from the Neurons in Action Tutorial that they modeled the addition of the pump as a change in the initial condition of the cell.
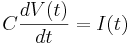

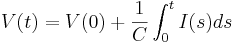
Add Leak Channels
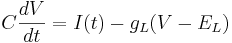
Leak channels add a resistor in parallel to the capacitor.
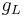 is the conductance of the channels
is the conductance of the channels
Add HH Channels