Difference between revisions of "NumHH"
(New page: == Numerical Solution of Differential Equations == Remember the equation for the cell with only leak channels. <math> C \frac{dV}{dt} = I(t) - g_L(V - E_L) </math> Let's simplify: suppo...) |
|||
| Line 19: | Line 19: | ||
The simplest way of solving this equation is with Euler's method: | The simplest way of solving this equation is with Euler's method: | ||
| − | <big> <big> <big> <math> y_k = y_{k-1} + | + | <big> <big> <big> <math> y_k = y_{k-1} + \Delta t \ (-k y_{k-1}) </math> </big> </big> </big> |
This is a special case of the general formula for Euler's method applied to the (vector) differential equation | This is a special case of the general formula for Euler's method applied to the (vector) differential equation | ||
Revision as of 19:37, 23 February 2009
Numerical Solution of Differential Equations
Remember the equation for the cell with only leak channels.
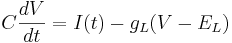
Let's simplify: suppose there is no injected current and that the reversal potential for the leak channels is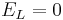 
. Then our equation is
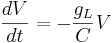
Using different letters for the variables (because this is done in the software linked below):
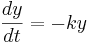
Here k is the rate constant, 1/k is the time constant, 1/k is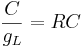 
in the notation above. A leaky cell is what is called an RC circuit -- a resistor and capacitor together in a circuit. The time constant of an RC circuit is RC. The bigger k, the higher the rate of convergence, and the smaller the time constant 1/k. The time constant is the time it takes the solution to decay to 1/e of its value.
Solution of differential equations happens at discrete times: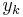 
, separated by small time intervals dt.
The simplest way of solving this equation is with Euler's method:
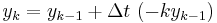
This is a special case of the general formula for Euler's method applied to the (vector) differential equation
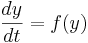
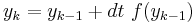
Euler's equation is the simplest way to solve a differential equation numerically. However it is often not the preferred method: often you need to take much smaller time steps with Euler than with some other methods, so it takes longer to get as good a solution. Still if you are doing something complicated, like solving an equation with noise, or Bayesian filtering (to compute likelihood), an argument can be made that a simpler method is desirable -- at least as a first step.
Click here for code for visualizing the numerical solution of differential equations.
