Difference between revisions of "NumericalDiffEqs"

From Sean_Carver
Jump to: navigation, search
Line 1: Line 1:
 +
== Equilibrium Potentials ==
 +
 +
You can find the equilibrium potential for given channel conductances.  Set the injected current to zero I = 0.  Then fix and absorb the gating variables and maximal conductances <math> (g_L, g_{Na}, g_{K}) </math> into single conductance variables <math> (G_L, G_{Na}, G_{K}) </math>.
 +
 +
For example
 +
 +
<math> G_{K} = n^4 g_K </math>
 +
 +
Then the differential equation for the membrane is
 +
 +
<math> C \frac{dV}{dt} = - G_L (V - E_L) - G_{Na} (V - E_{Na}) - G_K (V - E_K) </math>
 +
 +
The equilibrium potential is the value of V such that <math> \frac{dV}{dt} </math> is zero.  You can plug in <math> \frac{dV}{dt} = 0 </math> and solve for <math> V_{equilibrium}. </math>
 +
 +
<math> V_{equilibrium} = \frac{G_L E_L + G_{Na} E_{Na} + G_K E_K}{G_L + G_{Na} + G_K} </math>
 +
 +
The equilibrium potential is the weighted average of the reversal potentials -- weighted by the corresponding conductances.  Note that the weights add to one.
 +
 +
== Numerical Solution of Differential Equations ==
 +
 
Remember the equation for the cell with only leak channels.
 
Remember the equation for the cell with only leak channels.
  

Revision as of 23:37, 12 February 2009

Equilibrium Potentials

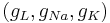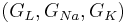You can find the equilibrium potential for given channel conductances. Set the injected current to zero I = 0. Then fix and absorb the gating variables and maximal conductances (g_L, g_{Na}, g_{K}) into single conductance variables (G_L, G_{Na}, G_{K}) .

For example

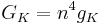
G_{K} = n^4 g_K

Then the differential equation for the membrane is

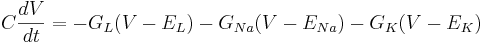
C \frac{dV}{dt} = - G_L (V - E_L) - G_{Na} (V - E_{Na}) - G_K (V - E_K)

The equilibrium potential is the value of V such that 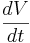\frac{dV}{dt} is zero. You can plug in 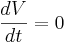\frac{dV}{dt} = 0 and solve for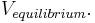 V_{equilibrium}.

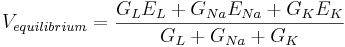
V_{equilibrium} = \frac{G_L E_L + G_{Na} E_{Na} + G_K E_K}{G_L + G_{Na} + G_K}

The equilibrium potential is the weighted average of the reversal potentials -- weighted by the corresponding conductances. Note that the weights add to one.

Numerical Solution of Differential Equations

Remember the equation for the cell with only leak channels.

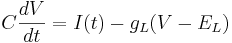
C \frac{dV}{dt} = I(t) - g_L(V - E_L)

Let's simplify: suppose there is no injected current and that the reversal potential for the leak channels is 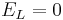E_L = 0 . Then our equation is

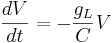
\frac{dV}{dt} = - \frac{g_L}{C} V

Using different letters for the variables (because this is done in the software linked below):

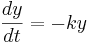
\frac{dy}{dt} = - k y

Here k is the rate constant, 1/k is the time constant, 1/k is 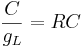\frac{C}{g_L} = RC in the notation above. A leaky cell is what is called an RC circuit -- a resistor and capacitor together in a circuit. The time constant of an RC circuit is RC. The bigger k, the higher the rate of convergence, and the smaller the time constant 1/k. The time constant is the time it takes the solution to decay to 1/e of its value.

Solution of differential equations happens at discrete times: 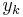y_k , separated by small time intervals dt.

The simplest way of solving this equation is with Euler's method:

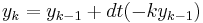
y_k = y_{k-1} + dt (-k y_{k-1})

This is a special case of the general formula for Euler's method applied to the (vector) differential equation

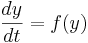
\frac{dy}{dt} = f(y)

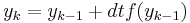
y_k = y_{k-1} + dt f(y_{k-1})

Click here for code for visualizing the numerical solution of differential equations.

Retrieved from "https://seancarver.org/index.php?title=NumericalDiffEqs&oldid=419"