Difference between revisions of "Chattering"
| (16 intermediate revisions by the same user not shown) | |||
| Line 3: | Line 3: | ||
First the [[Survey05|survey from before Spring Break]] | First the [[Survey05|survey from before Spring Break]] | ||
| − | Next the [[Media:Lab_N|homework due after Spring Break]]. | + | Next the [[Media:Lab_N.pdf|homework due after Spring Break]]. |
| − | Finally, today's tutorial will be the Chattering Ion Channels Tutorial from Neurons in Action. | + | Finally, today's tutorial will be the Chattering Ion Channels Tutorial from Neurons in Action. The purpose of today's tutorial is to prepare you for the lecture on Bayesian filtering. |
| − | |||
| − | The purpose of | ||
[[Image:Chattering_Screen_Shot.jpg|center|thumb|300px|Click image for full size]] | [[Image:Chattering_Screen_Shot.jpg|center|thumb|300px|Click image for full size]] | ||
| Line 13: | Line 11: | ||
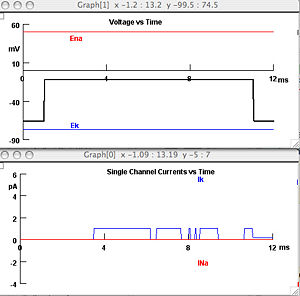
For today's tutorial you will generate figures that look like the one shown above. Experimentally, (i.e. with real cells and channels) such a figure would be generated with a "patch clamp," The patch clamp technique is described and illustrated very nicely in Neurons in Action. | For today's tutorial you will generate figures that look like the one shown above. Experimentally, (i.e. with real cells and channels) such a figure would be generated with a "patch clamp," The patch clamp technique is described and illustrated very nicely in Neurons in Action. | ||
| − | The ion channel problem | + | The ion channel problem relevant to Bayesian filtering is not discussed in Neuron's in Action. Here is the problem: we have an open state and a closed state and we want the probabilities of transitioning between them. For example, if you are in the open state, what is the probability of closing by the next time step? Probabilities make sense here because the data is sampled discretely. If you were doing this for real you would try to estimate reaction rates which is independent of the time step. Obviously probabilities increase as you increase the time step. But probabilities are simpler so we will fix the time step and just deal with probabilities. |
| + | |||
| + | If you can tell when transitions occur the problem is trivial. For example, the probability of switching from an open to a closed state is approximately: | ||
| + | |||
| + | <math> \mbox{probability open } \rightarrow \mbox{ closed} \approx \frac{ \mbox{number of open to closed transitions observed}}{ \mbox{ number of times observed in open state}} </math> | ||
| + | |||
| + | The problem is much harder if you cannot always discern what state the channel is in, nor when transitions occur. One way that this could happen is if the measurements were noisy -- so noisy that you couldn't reliably tell if the channel was open or closed. | ||
| + | |||
| + | An even more interesting scenario occurs when the channel has more than one state with the same conductance. Typically this happens when the channel has more than one closed state. Remember than most sodium channels are closed both before and after an action potential, but after an action potential many of them are in a different state -- they are inactive. With a patch clamp both the closed and the inactive states would look the same -- no current flowing through the channel. So what if you wanted to estimate probabilities (or reaction rates) for transitions between these same conductance states. | ||
| + | |||
| + | I have come up with a toy problem to study this. A toy problem is one inspired by an application (biology), but has been abstracted to make it easier to understand and work with. Here is the problem -- there is an open state (O) and closed state (C) and a stuck state (S). Transitions between these states happen like this | ||
| + | |||
| + | <math> O \rightleftharpoons C \rightleftharpoons S </math> | ||
| + | |||
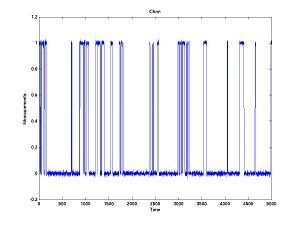
| + | Transitions between O and S never happen (i.e. the probability is negligible) without C being an intermediary state. The observed current is zero in C and S and one in O. And there is noise. We want to estimate the probability of transitioning back and forth between C and S. | ||
| + | |||
| + | Here is what some data might look like: | ||
| + | |||
| + | [[Image:Toy_Model_Simulation.jpg|center|thumb|300px|Click image for full size]] | ||
| + | |||
| + | In a future lecture/lab, we are going to use Bayesian filtering to solve this problem. | ||
| + | |||
| + | I want to say a few words about why I have chosen to illustrate Bayesian filtering with a channel model instead of the cell models we have been working on. This channel model has only three possible states O,C,S. The Hodgkin-Huxley model has a four dimensional continuum for the states (one dimension for the membrane potential and 3 for the activation variables). It is much easier to see what is happening in Bayesian filtering with only three states. The equations are much simpler! We will also talk about filtering the Hodgkin-Huxley model after we have developed intuition with our toy channel model. | ||
| + | |||
| + | But first we will learn about channel models with today's tutorial ... | ||
| + | |||
| + | '''Homework:''' Put three observations from today's tutorial into a PowerPoint and send to me. | ||
Latest revision as of 19:41, 24 March 2009
Welcome back everyone.
First the survey from before Spring Break
Next the homework due after Spring Break.
Finally, today's tutorial will be the Chattering Ion Channels Tutorial from Neurons in Action. The purpose of today's tutorial is to prepare you for the lecture on Bayesian filtering.
For today's tutorial you will generate figures that look like the one shown above. Experimentally, (i.e. with real cells and channels) such a figure would be generated with a "patch clamp," The patch clamp technique is described and illustrated very nicely in Neurons in Action.
The ion channel problem relevant to Bayesian filtering is not discussed in Neuron's in Action. Here is the problem: we have an open state and a closed state and we want the probabilities of transitioning between them. For example, if you are in the open state, what is the probability of closing by the next time step? Probabilities make sense here because the data is sampled discretely. If you were doing this for real you would try to estimate reaction rates which is independent of the time step. Obviously probabilities increase as you increase the time step. But probabilities are simpler so we will fix the time step and just deal with probabilities.
If you can tell when transitions occur the problem is trivial. For example, the probability of switching from an open to a closed state is approximately:
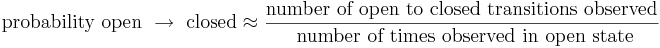
The problem is much harder if you cannot always discern what state the channel is in, nor when transitions occur. One way that this could happen is if the measurements were noisy -- so noisy that you couldn't reliably tell if the channel was open or closed.
An even more interesting scenario occurs when the channel has more than one state with the same conductance. Typically this happens when the channel has more than one closed state. Remember than most sodium channels are closed both before and after an action potential, but after an action potential many of them are in a different state -- they are inactive. With a patch clamp both the closed and the inactive states would look the same -- no current flowing through the channel. So what if you wanted to estimate probabilities (or reaction rates) for transitions between these same conductance states.
I have come up with a toy problem to study this. A toy problem is one inspired by an application (biology), but has been abstracted to make it easier to understand and work with. Here is the problem -- there is an open state (O) and closed state (C) and a stuck state (S). Transitions between these states happen like this
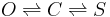
Transitions between O and S never happen (i.e. the probability is negligible) without C being an intermediary state. The observed current is zero in C and S and one in O. And there is noise. We want to estimate the probability of transitioning back and forth between C and S.
Here is what some data might look like:
In a future lecture/lab, we are going to use Bayesian filtering to solve this problem.
I want to say a few words about why I have chosen to illustrate Bayesian filtering with a channel model instead of the cell models we have been working on. This channel model has only three possible states O,C,S. The Hodgkin-Huxley model has a four dimensional continuum for the states (one dimension for the membrane potential and 3 for the activation variables). It is much easier to see what is happening in Bayesian filtering with only three states. The equations are much simpler! We will also talk about filtering the Hodgkin-Huxley model after we have developed intuition with our toy channel model.
But first we will learn about channel models with today's tutorial ...
Homework: Put three observations from today's tutorial into a PowerPoint and send to me.