Difference between revisions of "DiffEqs"
(→Add Leak Channels) |
|||
| (13 intermediate revisions by the same user not shown) | |||
| Line 1: | Line 1: | ||
| + | Based on the results from [[Survey03|Tuesday's survey]], today's lab will be the Neuron's in Action Equilibrium Potential Lab. | ||
| + | |||
| + | * '''Homework F:''' Make three observations from the Tutorial and write them up. Include a bonus, if you like. | ||
| + | |||
| + | Before we start the lab, let's talk about [[Media:Lab_E.pdf|Lab E Homework]] and the equations behind this week's labs. It is important to be able to recognize these equations and know what they mean if you ever read modeling papers or code your own models. | ||
| + | |||
== Plain Bilayer Membrane == | == Plain Bilayer Membrane == | ||
| Line 9: | Line 15: | ||
Here ''C'' is a constant (a parameter): the ''capacitance'' of the membrane. | Here ''C'' is a constant (a parameter): the ''capacitance'' of the membrane. | ||
| − | Next ''V(t)'' is the membrane potential. Typically ''V(t)'' is the quantity of interest -- and it is the quantity that is usually | + | Next ''V(t)'' is the membrane potential. Typically ''V(t)'' is the quantity of interest -- and it is the quantity that is usually measured. |
| − | Next ''I(t)'' is the capacitive current into the cell. In general the capacitive current involves the ionic currents into the cell as well as the injected current, but for a plain lipid bilayer, it is just the injected current. | + | Next ''I(t)'' is the capacitive current into the cell. In general the capacitive current involves the ionic currents into the cell as well as the injected current, but for a plain lipid bilayer, it is just the injected current -- which is specified by the experimenter. |
Finally ''V(0)'' is the initial membrane potential of the cell, the constant of integration required for a definite solution to the equation. | Finally ''V(0)'' is the initial membrane potential of the cell, the constant of integration required for a definite solution to the equation. | ||
| Line 48: | Line 54: | ||
<math> C \frac{dV}{dt} = I(t) - g_L (V(t) - E_L) - g_{Na} m^3(t) h(t) (V(t) - E_{Na}) - g_K n^4(t) (V(t) - E_K) </math> | <math> C \frac{dV}{dt} = I(t) - g_L (V(t) - E_L) - g_{Na} m^3(t) h(t) (V(t) - E_{Na}) - g_K n^4(t) (V(t) - E_K) </math> | ||
| + | |||
| + | In addition to the leak current there is now a sodium current and a potassium current. These add similar terms to the capacitive current: | ||
| + | |||
| + | Leak: <math> g_L (V(t) - E_L) </math> | ||
| + | |||
| + | Sodium: <math> g_{Na} m^3(t) h(t) (V(t) - E_{Na}) </math> | ||
| + | |||
| + | Potassium: <math> g_K n^4(t) (V(t) - E_K) </math> | ||
| + | |||
| + | Sodium gating variables: <math> m^3(t) h(t) </math> | ||
| + | |||
| + | Potassium gating variables: <math> n^4(t) </math> | ||
| + | |||
| + | Sodium has three activation gates (m's) and one inactivation gate (h). | ||
| + | |||
| + | Potassium has four activation gates (n's). | ||
| + | |||
| + | The activation variables m(t), h(t), n(t) are always (for all times t) numbers between 0 and 1. They represent the fraction of gates that are in the open position. All four gates must be open for the channel to conduct. Take the potassium current: it has four gates with the same kinetics. We could model this as a(t)*b(t)*c(t)*d(t) instead of n^4(t), but by symmetry we don't expect a,b,c,d to be different, so to avoid the complication we just take n^4. | ||
| + | |||
| + | If n(t) = 0.1 then 10% of the gates are open. But for an individual channel, all four of its gates must be open to conduct so 1 in 10000 conduct and the potassium conductance is (0.1^4) = 1/10000 its maximal conductance when all channels are open. | ||
| + | |||
| + | To perform a Hodgkin-Huxley simulation we need to keep track of m,h,n in addition to V. These four variables are the state variables for the equation. There are differential equations that govern how these variables change | ||
| + | |||
| + | <math> \frac{dm}{dt} = \cdots </math> | ||
| + | |||
| + | <math> \frac{dh}{dt} = \cdots </math> | ||
| + | |||
| + | <math> \frac{dn}{dt} = \cdots </math> | ||
| + | |||
| + | If you fix the membrane potential (i.e. voltage clamp) m,n, & h have an asymptotic value (between 0 and 1) and a time constant - m,n,h approach their asymptotic value at a rate determined by the time constant. But both the asymptotic value and time constant depend on membrane potential -- just as the rate of change of the membrane potential depends on m, n, & h. This is called coupling between differential equations. | ||
| + | |||
| + | == Equilibrium Potentials == | ||
| + | |||
| + | You can find the equilibrium potential for given channel conductances. Set the injected current to zero I = 0. Then fix and absorb the gating variables and maximal conductances <math> (g_L, g_{Na}, g_{K}) </math> into single conductance variables <math> (G_L, G_{Na}, G_{K}) </math>. | ||
| + | |||
| + | For example | ||
| + | |||
| + | <math> G_{K} = n^4 g_K </math> | ||
| + | |||
| + | Then the differential equation for the membrane is | ||
| + | |||
| + | <math> C \frac{dV}{dt} = - G_L (V - E_L) - G_{Na} (V - E_{Na}) - G_K (V - E_K) </math> | ||
| + | |||
| + | The equilibrium potential is the value of V such that <math> \frac{dV}{dt} </math> is zero. You can plug in <math> \frac{dV}{dt} = 0 </math> and solve for <math> V_{equilibrium}. </math> | ||
| + | |||
| + | <math> V_{equilibrium} = \frac{G_L E_L + G_{Na} E_{Na} + G_K E_K}{G_L + G_{Na} + G_K} </math> | ||
| + | |||
| + | The equilibrium potential is the weighted average of the reversal potentials -- weighted by the corresponding conductances. Note that the weights add to one. | ||
Latest revision as of 21:05, 12 February 2009
Based on the results from Tuesday's survey, today's lab will be the Neuron's in Action Equilibrium Potential Lab.
- Homework F: Make three observations from the Tutorial and write them up. Include a bonus, if you like.
Before we start the lab, let's talk about Lab E Homework and the equations behind this week's labs. It is important to be able to recognize these equations and know what they mean if you ever read modeling papers or code your own models.
Contents
Plain Bilayer Membrane
Remember the capacitor equation:
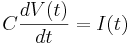
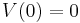
Here C is a constant (a parameter): the capacitance of the membrane.
Next V(t) is the membrane potential. Typically V(t) is the quantity of interest -- and it is the quantity that is usually measured.
Next I(t) is the capacitive current into the cell. In general the capacitive current involves the ionic currents into the cell as well as the injected current, but for a plain lipid bilayer, it is just the injected current -- which is specified by the experimenter.
Finally V(0) is the initial membrane potential of the cell, the constant of integration required for a definite solution to the equation.
We can solve this equation
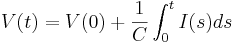
Add Na+/K+ Pump
It seems clear from the Neurons in Action Tutorial that they modeled the addition of the pump as a change in the initial condition of the cell.
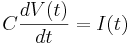

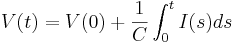
Add Leak Channels
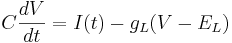
Leak channels add a resistor in parallel to the capacitor.
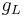 is the conductance of the channels (which is the reciprocal of the resistance of the channels).
is the conductance of the channels (which is the reciprocal of the resistance of the channels).
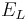 is the reversal potential of the leak current.
is the reversal potential of the leak current.
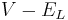 is the driving potential.
is the driving potential.
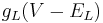 is the current across the resistor (Ohm's Law).
is the current across the resistor (Ohm's Law).
The resistive current is minus its contribution to the capacitive current (Kirchov's Law).
Add HH Channels
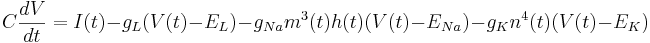
In addition to the leak current there is now a sodium current and a potassium current. These add similar terms to the capacitive current:
Leak: 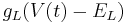
Sodium: 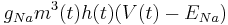
Potassium: 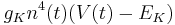
Sodium gating variables: 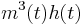
Potassium gating variables: 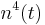
Sodium has three activation gates (m's) and one inactivation gate (h).
Potassium has four activation gates (n's).
The activation variables m(t), h(t), n(t) are always (for all times t) numbers between 0 and 1. They represent the fraction of gates that are in the open position. All four gates must be open for the channel to conduct. Take the potassium current: it has four gates with the same kinetics. We could model this as a(t)*b(t)*c(t)*d(t) instead of n^4(t), but by symmetry we don't expect a,b,c,d to be different, so to avoid the complication we just take n^4.
If n(t) = 0.1 then 10% of the gates are open. But for an individual channel, all four of its gates must be open to conduct so 1 in 10000 conduct and the potassium conductance is (0.1^4) = 1/10000 its maximal conductance when all channels are open.
To perform a Hodgkin-Huxley simulation we need to keep track of m,h,n in addition to V. These four variables are the state variables for the equation. There are differential equations that govern how these variables change
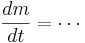
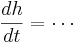
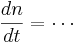
If you fix the membrane potential (i.e. voltage clamp) m,n, & h have an asymptotic value (between 0 and 1) and a time constant - m,n,h approach their asymptotic value at a rate determined by the time constant. But both the asymptotic value and time constant depend on membrane potential -- just as the rate of change of the membrane potential depends on m, n, & h. This is called coupling between differential equations.
Equilibrium Potentials
You can find the equilibrium potential for given channel conductances. Set the injected current to zero I = 0. Then fix and absorb the gating variables and maximal conductances 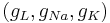 into single conductance variables
into single conductance variables 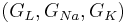 .
.
For example
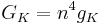
Then the differential equation for the membrane is
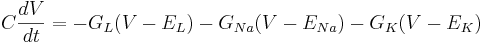
The equilibrium potential is the value of V such that 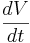 is zero. You can plug in
is zero. You can plug in 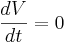 and solve for
and solve for 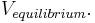
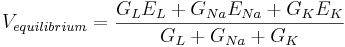
The equilibrium potential is the weighted average of the reversal potentials -- weighted by the corresponding conductances. Note that the weights add to one.