Difference between revisions of "Using Mediawiki In The Classroom"
From Sean_Carver
| (One intermediate revision by the same user not shown) | |||
| Line 1: | Line 1: | ||
* '''I find it very easy to develop then deliver lectures with Mediawiki''' | * '''I find it very easy to develop then deliver lectures with Mediawiki''' | ||
| + | * Can copy and paste text and images from other Mediawiki websites (e.g. Wikipedia) provided the license allows (generally OK with Wikipedia text, often OK with images, but see license) | ||
* Mediawiki has well tested, powerful features, (It runs Wikipedia), | * Mediawiki has well tested, powerful features, (It runs Wikipedia), | ||
Including: | Including: | ||
| − | * Tex formula, e.g. fundamental theorem of calculus: | + | * Tex formula, e.g. fundamental theorem of calculus (copied from [http://en.wikipedia.org/w/index.php?title=Fundamental_theorem_of_calculus&oldid=417680255 here]): |
Let ''ƒ'' be a continuous real-valued function defined on a closed interval [''a'', ''b'']. Let ''F'' be the function defined, for all ''x'' in [''a'', ''b''], by | Let ''ƒ'' be a continuous real-valued function defined on a closed interval [''a'', ''b'']. Let ''F'' be the function defined, for all ''x'' in [''a'', ''b''], by | ||
Latest revision as of 17:04, 1 December 2011
- I find it very easy to develop then deliver lectures with Mediawiki
- Can copy and paste text and images from other Mediawiki websites (e.g. Wikipedia) provided the license allows (generally OK with Wikipedia text, often OK with images, but see license)
- Mediawiki has well tested, powerful features, (It runs Wikipedia),
Including:
- Tex formula, e.g. fundamental theorem of calculus (copied from here):
Let ƒ be a continuous real-valued function defined on a closed interval [a, b]. Let F be the function defined, for all x in [a, b], byThen, F is continuous on [a, b], differentiable on the open interval (a, b), and
for all x in (a, b).
- Images
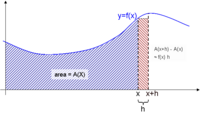The area shaded in red stripes can be estimated as h times ƒ(x). Alternatively, if the function A(x) were known, it could be computed as A(x + h) − A(x). These two values are approximately equal, particularly for small h. Copyright - Links to other websites (e.g. Fundamental Theorem of Calculus)
- Links to other pages within Class notes (e.g. surveys).
- Powerpoint slides (e.g. homework)
- Code (to download or cut and paste into Matlab, Maple, or Mathematica, etc. See my lecture on Bayesian Filtering)
Additionally, Mediawiki is
- Free and open source
- Collaborative (e.g. Instructor and TAs can have, but students need not have, edit privileges)
