Difference between revisions of "Using Mediawiki In The Classroom"
From Sean_Carver
| (32 intermediate revisions by the same user not shown) | |||
| Line 1: | Line 1: | ||
| − | * Mediawiki has well tested, powerful features | + | * '''I find it very easy to develop then deliver lectures with Mediawiki''' |
| − | * ''' | + | * Can copy and paste text and images from other Mediawiki websites (e.g. Wikipedia) provided the license allows (generally OK with Wikipedia text, often OK with images, but see license) |
| + | * Mediawiki has well tested, powerful features, (It runs Wikipedia), | ||
| + | |||
| + | Including: | ||
| + | |||
| + | * Tex formula, e.g. fundamental theorem of calculus (copied from [http://en.wikipedia.org/w/index.php?title=Fundamental_theorem_of_calculus&oldid=417680255 here]): | ||
| + | |||
| + | Let ''ƒ'' be a continuous real-valued function defined on a closed interval [''a'', ''b'']. Let ''F'' be the function defined, for all ''x'' in [''a'', ''b''], by | ||
| + | <math>F(x) = \int_a^x f(t)\, dt\,.</math> | ||
| + | Then, ''F'' is continuous on [''a'', ''b''], differentiable on the open interval (''a'', ''b''), and | ||
| + | <math>F'(x) = f(x)\,</math> | ||
| + | for all ''x'' in (''a'', ''b''). | ||
| + | |||
| + | * Images [[Image:FTC geometric.png|200px|thumb|center|The area shaded in red stripes can be estimated as ''h'' times ''ƒ''(''x''). Alternatively, if the function ''A''(''x'') were known, it could be computed as ''A''(''x'' + ''h'') − ''A''(''x''). These two values are approximately equal, particularly for small ''h''. [http://en.wikipedia.org/w/index.php?title=File:FTC_geometric.png&oldid=376032010 Copyright]]] | ||
| + | * Links to other websites (e.g. [http://en.wikipedia.org/wiki/Fundamental_theorem_of_calculus Fundamental Theorem of Calculus]) | ||
| + | * Links to other pages within Class notes (e.g. [[Survey01|surveys]]). | ||
| + | * Powerpoint slides (e.g. [[Media:Lab_W.pdf|homework]]) | ||
| + | * Code (to download or cut and paste into Matlab, Maple, or Mathematica, etc. [[Bayesian Filtering|See my lecture on Bayesian Filtering]]) | ||
| + | |||
| + | Additionally, Mediawiki is | ||
| + | |||
| + | * Free and open source | ||
| + | * Collaborative (e.g. Instructor and TAs can have, but students need not have, edit privileges) | ||
Latest revision as of 17:04, 1 December 2011
- I find it very easy to develop then deliver lectures with Mediawiki
- Can copy and paste text and images from other Mediawiki websites (e.g. Wikipedia) provided the license allows (generally OK with Wikipedia text, often OK with images, but see license)
- Mediawiki has well tested, powerful features, (It runs Wikipedia),
Including:
- Tex formula, e.g. fundamental theorem of calculus (copied from here):
Let ƒ be a continuous real-valued function defined on a closed interval [a, b]. Let F be the function defined, for all x in [a, b], byThen, F is continuous on [a, b], differentiable on the open interval (a, b), and
for all x in (a, b).
- Images
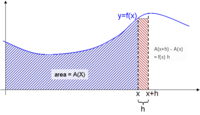The area shaded in red stripes can be estimated as h times ƒ(x). Alternatively, if the function A(x) were known, it could be computed as A(x + h) − A(x). These two values are approximately equal, particularly for small h. Copyright - Links to other websites (e.g. Fundamental Theorem of Calculus)
- Links to other pages within Class notes (e.g. surveys).
- Powerpoint slides (e.g. homework)
- Code (to download or cut and paste into Matlab, Maple, or Mathematica, etc. See my lecture on Bayesian Filtering)
Additionally, Mediawiki is
- Free and open source
- Collaborative (e.g. Instructor and TAs can have, but students need not have, edit privileges)
