Difference between revisions of "Using Mediawiki In The Classroom"
From Sean_Carver
| Line 5: | Line 5: | ||
* Tex formula | * Tex formula | ||
| + | |||
| + | Let ''ƒ'' be a continuous real-valued function defined on a [[Interval (mathematics)#Terminology|closed interval]] [''a'', ''b'']. Let ''F'' be the function defined, for all ''x'' in [''a'', ''b''], by | ||
| + | :<math>F(x) = \int_a^x f(t)\, dt\,.</math> | ||
| + | Then, ''F'' is continuous on [''a'', ''b''], differentiable on the open interval (''a'', ''b''), and | ||
| + | |||
| + | :<math>F'(x) = f(x)\,</math> | ||
| + | |||
| + | for all ''x'' in (''a'', ''b''). | ||
| + | |||
* Links to other websites | * Links to other websites | ||
* Links to other pages within Class notes | * Links to other pages within Class notes | ||
* Powerpoint slides | * Powerpoint slides | ||
* Code (to download or cut and paste into Matlab, Maple, or Mathematica, etc.) | * Code (to download or cut and paste into Matlab, Maple, or Mathematica, etc.) | ||
Revision as of 22:41, 13 March 2011
- I find it very easy to develop then deliver lectures with Mediawiki
- Mediawiki has well tested, powerful features, (It runs Wikipedia),
Including:
- Tex formula
Let ƒ be a continuous real-valued function defined on a closed interval [a, b]. Let F be the function defined, for all x in [a, b], by :Then, F is continuous on [a, b], differentiable on the open interval (a, b), and
: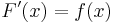
for all x in (a, b).
- Links to other websites
- Links to other pages within Class notes
- Powerpoint slides
- Code (to download or cut and paste into Matlab, Maple, or Mathematica, etc.)