Difference between revisions of "Bayesian Filtering"
| Line 48: | Line 48: | ||
[[Image:Seed12Fit.jpg|center|thumb|300px|Click image for full size]] | [[Image:Seed12Fit.jpg|center|thumb|300px|Click image for full size]] | ||
| + | |||
| + | I was concerned about the first plot, until I plotted the next two. Then I realized that the algorithm tries to estimate the probabilities of relatively rare events based on a limited amount of data (5000 data points). The performance may not look great at first sight, but consider how subtle are the inferences that it is trying to make. The estimates are reasonably close ... at least within the ballpark. It would look better zoomed out. With a lot more data, one can expect the estimates to be much better. | ||
| + | |||
| + | The purpose of the lecture is to present the Bayesian filtering algorithm. | ||
| + | |||
| + | == Prerequisites == | ||
Revision as of 16:47, 8 April 2009
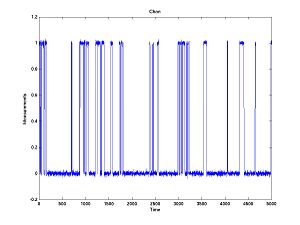
Here is the problem -- there is an open state (O) and closed state (C) and a stuck (inactivated) state (S). Transitions between these states happen like this
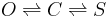
Transitions between O and S never happen (i.e. the probability is negligible) without C being an intermediary state. The observed current is zero in C and S and one in O. And there is noise. Transitions between C and S are invisible because there is no change in current. We want to estimate the transition probabilities. (The probabilities will depend upon the time step, but say the time step is fixed).
First generate some data which looks like.
The transition probabilities for this plot are
Probability(Stay in Open) = 0.95 Probability(Open --> Closed) = 0.05 Probability(Open --> Stuck/Inactive) = 0.00 Probability(Closed --> Open) = 0.10 Probability(Stay in Closed) = 0.85 Probability(Closed --> Stuck) = 0.05 Probability(Stuck --> Open) = 0.00 Probability(Stuck -- Closed) = 0.003 Probability(Stay in Stuck) = 0.097
There are nine parameters here, but there is a constraint that each block add to 1, so we only have 6 parameter to estimate. Moreover we might know that transition between open and stuck never happen, so there would only be 4 parameters to estimate.
Thus the likelihood function is a function from four parameters to one value (likelihood). Too many to plot. Let's say we know the probabilities of going back and forth between open and closed. Thus we need only know the probabilities of going back and forth between closed and stuck (the invisible transitions).
We are going to compute the likelihood as we vary
P(Stuck --> Closed) from 0.001 to 0.010 P(Closed --> Stuck) from 0.01 to 0.12
Actually, the way I wrote the program it computes
P(Stuck --> Closed) from 0.001 to 0.010 P(Stay in Closed) from 0.01 to 0.12
The two are equivalent because P(Closed --> Open) is correctly known and the three "from Closed" probabilities add to 1.
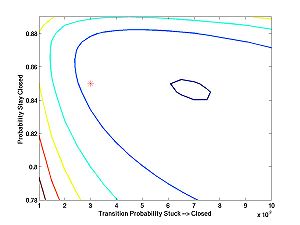
Here are what it looks like:
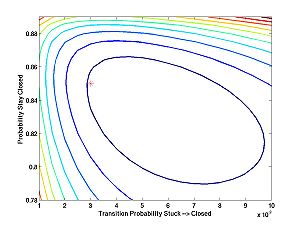
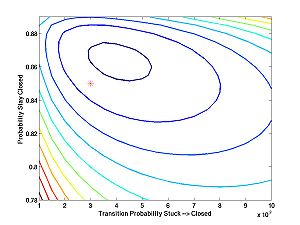
And with two different seeds:
I was concerned about the first plot, until I plotted the next two. Then I realized that the algorithm tries to estimate the probabilities of relatively rare events based on a limited amount of data (5000 data points). The performance may not look great at first sight, but consider how subtle are the inferences that it is trying to make. The estimates are reasonably close ... at least within the ballpark. It would look better zoomed out. With a lot more data, one can expect the estimates to be much better.
The purpose of the lecture is to present the Bayesian filtering algorithm.