Difference between revisions of "Bayesian Filtering"
| Line 25: | Line 25: | ||
There are nine parameters here, but there is a constraint that each block add to 1, so we only have 6 parameter to estimate. Moreover we might know that transition between open and stuck never happen, so there would only be 4 parameters to estimate. | There are nine parameters here, but there is a constraint that each block add to 1, so we only have 6 parameter to estimate. Moreover we might know that transition between open and stuck never happen, so there would only be 4 parameters to estimate. | ||
| − | Thus the likelihood function is a function from four parameters to one value (likelihood). Too many to plot. Let's say we know the probabilities of going back and forth between open and closed. Thus we need only know the probabilities of going back and forth between closed and stuck. | + | Thus the likelihood function is a function from four parameters to one value (likelihood). Too many to plot. Let's say we know the probabilities of going back and forth between open and closed. Thus we need only know the probabilities of going back and forth between closed and stuck (the invisible transitions). |
| + | |||
| + | We are going to compute the likelihood as we vary | ||
| + | |||
| + | P(Stuck --> Closed) from 0.001 to 0.010 | ||
| + | P(Closed --> Stuck) from 0.01 to 0.12 | ||
Revision as of 00:38, 8 April 2009
Here is the problem -- there is an open state (O) and closed state (C) and a stuck (inactivated) state (S). Transitions between these states happen like this
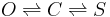
Transitions between O and S never happen (i.e. the probability is negligible) without C being an intermediary state. The observed current is zero in C and S and one in O. And there is noise. Transitions between C and S are invisible because there is no change in current. We want to estimate the transition probabilities. (The probabilities will depend upon the time step, but say the time step is fixed).
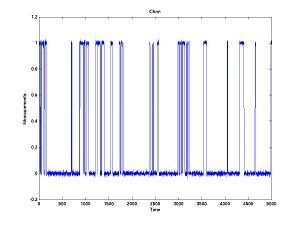
First generate some data which looks like.
The transition probabilities for this plot are
Probability(Stay in Open) = 0.95 Probability(Open --> Closed) = 0.05 Probability(Open --> Stuck/Inactive) = 0.00 Probability(Closed --> Open) = 0.10 Probability(Stay in Closed) = 0.85 Probability(Closed --> Stuck) = 0.05 Probability(Stuck --> Open) = 0.00 Probability(Stuck -- Closed) = 0.003 Probability(Stay in Stuck) = 0.097
There are nine parameters here, but there is a constraint that each block add to 1, so we only have 6 parameter to estimate. Moreover we might know that transition between open and stuck never happen, so there would only be 4 parameters to estimate.
Thus the likelihood function is a function from four parameters to one value (likelihood). Too many to plot. Let's say we know the probabilities of going back and forth between open and closed. Thus we need only know the probabilities of going back and forth between closed and stuck (the invisible transitions).
We are going to compute the likelihood as we vary
P(Stuck --> Closed) from 0.001 to 0.010 P(Closed --> Stuck) from 0.01 to 0.12