Difference between revisions of "Bayesian Filtering"
From Sean_Carver
(New page: Here is the problem -- there is an open state (O) and closed state (C) and a stuck (inactivated) state (S). Transitions between these states happen like this <math> O \rightleftharpoons ...) |
|||
| Line 3: | Line 3: | ||
<math> O \rightleftharpoons C \rightleftharpoons S </math> | <math> O \rightleftharpoons C \rightleftharpoons S </math> | ||
| − | Transitions between O and S never happen (i.e. the probability is negligible) without C being an intermediary state. The observed current is zero in C and S and one in O. And there is noise. We want to estimate the probability of transitioning back and forth between C and S | + | Transitions between O and S never happen (i.e. the probability is negligible) without C being an intermediary state. The observed current is zero in C and S and one in O. And there is noise. We want to estimate the probability of transitioning back and forth between C and S. Let's say we know everything else (i.e. the probabilities of transitioning back and forth between open and closed states). |
| − | + | First generate some data which looks like. | |
[[Image:Toy_Model_Simulation.jpg|center|thumb|300px|Click image for full size]] | [[Image:Toy_Model_Simulation.jpg|center|thumb|300px|Click image for full size]] | ||
| + | |||
| + | The transition probabilities for this plot are | ||
| + | |||
| + | Probability(Stay in Open) = 0.95 | ||
| + | Probability(Open --> Closed) = 0.05 | ||
| + | Probability(Open --> Stuck/Inactive) = 0.00 | ||
| + | |||
| + | Probability(Closed --> Open) = 0.10 | ||
| + | Probability(Stay in Closed) = 0.85 | ||
| + | Probability(Closed --> Stuck) = 0.05 | ||
| + | |||
| + | Probability(Stuck --> Open) = 0.00 | ||
| + | Probability(Stuck -- Closed) = 0.003 | ||
| + | Probability(Stay in Stuck) = 0.097 | ||
Revision as of 00:15, 8 April 2009
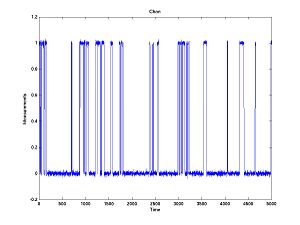
Here is the problem -- there is an open state (O) and closed state (C) and a stuck (inactivated) state (S). Transitions between these states happen like this
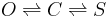
Transitions between O and S never happen (i.e. the probability is negligible) without C being an intermediary state. The observed current is zero in C and S and one in O. And there is noise. We want to estimate the probability of transitioning back and forth between C and S. Let's say we know everything else (i.e. the probabilities of transitioning back and forth between open and closed states).
First generate some data which looks like.
The transition probabilities for this plot are
Probability(Stay in Open) = 0.95 Probability(Open --> Closed) = 0.05 Probability(Open --> Stuck/Inactive) = 0.00 Probability(Closed --> Open) = 0.10 Probability(Stay in Closed) = 0.85 Probability(Closed --> Stuck) = 0.05 Probability(Stuck --> Open) = 0.00 Probability(Stuck -- Closed) = 0.003 Probability(Stay in Stuck) = 0.097