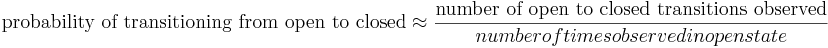Difference between revisions of "Chattering"
| Line 17: | Line 17: | ||
If you can tell when transitions occur the problem is trivial. For example, the probability of switching from an open to a closed state is approximately: | If you can tell when transitions occur the problem is trivial. For example, the probability of switching from an open to a closed state is approximately: | ||
| − | <math> \frac{ \mbox{number of open to closed transitions observed}}{ | + | <math> \mbox{probability of transitioning from open to closed} \approx \frac{ \mbox{number of open to closed transitions observed}}{ number of times observed in open state} </math> |
Revision as of 13:27, 24 March 2009
Welcome back everyone.
First the survey from before Spring Break
Next the homework due after Spring Break.
Finally, today's tutorial will be the Chattering Ion Channels Tutorial from Neurons in Action.
The purpose of this tutorial is to prepare you for the lecture on Bayesian filtering.
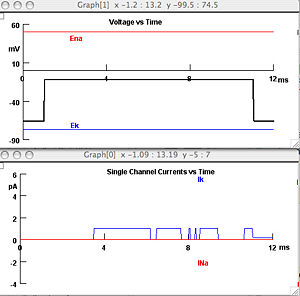
For today's tutorial you will generate figures that look like the one shown above. Experimentally, (i.e. with real cells and channels) such a figure would be generated with a "patch clamp," The patch clamp technique is described and illustrated very nicely in Neurons in Action.
The ion channel problem I am really interested in is not discussed in Neuron's in Action. Here is the problem: we have an open state an a closed state and we want the probabilities of transitioning between them. For example, if you are in the open state, what is the probability of closing by the next time step. Probabilities make sense here because the data is sampled discretely. If you were doing this for real you would try to estimate reaction rates which is independent of the time step. Obviously probabilities increase as you increase the time step. But probabilities are simpler so we will fix the time step and just deal with probabilities.
If you can tell when transitions occur the problem is trivial. For example, the probability of switching from an open to a closed state is approximately: