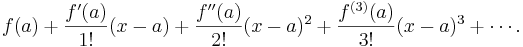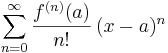Taylor Series
From Sean_Carver
Review Concepts
- Sequences
- Convergence
- Infinite series
- The sequence of partial sums of an infinite series
- Power series
New Concept: Taylor Series
- Think of Taylor series as a special kind of power series, where the sequence of partial sums are meant as better and better approximations of some other function.
- The Taylor Series is derived from the function.
Definition copied, verified, and adapted from Wikipedia, this page (permanent link). See license to copy, modify, distribute.
The Taylor series of a function ƒ(x) at a is the power series
which can be written in the more compact sigma notation as
- Convergence: A function whose Taylor series converges to the function is called analytic. But sometimes, as we have seen with power series generally, convergence can occur only within a radius of convergence.
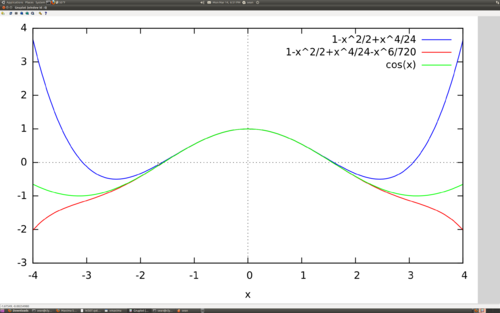
- Example: The Taylor series for cos(x), at a = 0. Partial sums for 4 and 6 terms.
Try it yourself
Open Maxima and type (or copy and paste):
a:0; n1:4; n2:6; M:4; plot2d([taylor(cos(x),x,a,n1), taylor(cos(x),x,a,n2), cos(x)],[x,-M,M]);
After you have typed in the above you can change the parameters a, n1, n2, M by scrolling up and changing them, then pressing return.