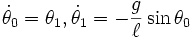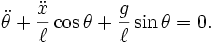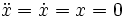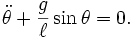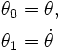Difference between revisions of "Matlab Primer"
(→Step 1: Make the model first order) |
(→Step 1: Make the model first order) |
||
| Line 28: | Line 28: | ||
Define new variables | Define new variables | ||
| − | :<math>\theta_0 & = \theta, \\ | + | :<math>\begin{align} |
| − | \theta_1 & = \dot\theta </math> | + | \theta_0 & = \theta, \\ |
| + | \theta_1 & = \dot\theta \end{align} </math> | ||
Now we have two equations: | Now we have two equations: | ||
Revision as of 18:29, 3 November 2012
Today's lecture will be on MATLAB and PENDULA (plural of PENDULUM). Your next lab assignment motivated the topic.
My name is Sean Carver; I am a research scientist in Mechanical Engineering. I have been programming in MATLAB for almost 20 years and programming computers for almost 30 years.
This class is about MATLAB, not about deriving equations. So I am just going to give you the equations for the PENDULUM. There is still a lot to do to get it into MATLAB.
Pendulum on a movable support
This example comes from Wikipedia (copied legally). Consider a pendulum of mass m and length ℓ, which is attached to a support with mass M which can move along a line in the x-direction. Let x be the coordinate along the line of the support, and let us denote the position of the pendulum by the angle θ from the vertical.
See http://en.wikipedia.org/w/index.php?title=Lagrangian_mechanics&oldid=516894618 for a full derivation.
Your homework and class exercise for today is to implement this model.
Pendulum on a fixed support
Together we are going to implement a simpler model with support fixed and unmovable. You can see what the equations for this are easily. Just plug in
The second term drops out:
Step 1: Make the model first order
Define new variables
Now we have two equations: