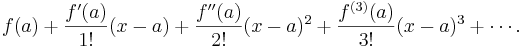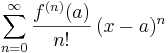Difference between revisions of "Taylor Series"
From Sean_Carver
(→New Concept: Taylor Series) |
(→New Concept: Taylor Series) |
||
| Line 12: | Line 12: | ||
* The Taylor Series is derived from the function. | * The Taylor Series is derived from the function. | ||
| − | Definition copied, verified, and adapted from Wikipedia, [http://en.wikipedia.org/w/index.php?title=Taylor_series&oldid=418169005 this page (permanent link)] | + | Definition copied, verified, and adapted from Wikipedia, [http://en.wikipedia.org/w/index.php?title=Taylor_series&oldid=418169005 this page (permanent link)]. See [http://en.wikipedia.org/wiki/Wikipedia:Text_of_the_GNU_Free_Documentation_License license to copy, modify, distribute.] |
The Taylor series of a function ''ƒ''(''x'') at ''a'' is the power series | The Taylor series of a function ''ƒ''(''x'') at ''a'' is the power series | ||
Revision as of 21:39, 14 March 2011
Review Concepts
- Sequences
- Convergence
- Infinite series
- The sequence of partial sums of an infinite series
- Power series
New Concept: Taylor Series
- Think of Taylor series as a special kind of power series, where the sequence of partial sums are meant as better and better approximations of some other function.
- The Taylor Series is derived from the function.
Definition copied, verified, and adapted from Wikipedia, this page (permanent link). See license to copy, modify, distribute.
The Taylor series of a function ƒ(x) at a is the power series
which can be written in the more compact sigma notation as